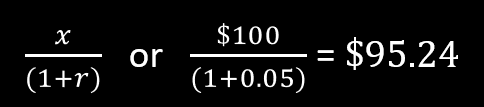Time Value of Money

One simple concept underpins all of finance: a dollar today is worth more than a dollar tomorrow. If you remember nothing else, remember that.

Why is that? It is because time has real value and it is the one constant and guaranteed variable in existence. This time-value presents optionality for your dollars, which we can assign value to.

• If I have a dollar today, I have the option of deciding what to do with it today, or tomorrow

• If instead I can only receive a dollar tomorrow, I’ve lost the option to decide what to do with it today, and that lost optionality has value

We’ll abbreviate it TVM (Time Value of Money) from here on out

TVM as the Foundation of Valuation

Since time is the one universal and unmovable constant in life, we can use it as the baseline when assigning value to our resources

When comparing the value of a dollar today to a dollar tomorrow, that baseline change, since we lost the optionality of a day, is called the discount rate.

In valuation, the discount rate is always displayed as an annual rate, and most types of analysis are done at an annual level for reasons of practicality and feasibility. From here on out all rates will be annual rates unless otherwise noted, and whenever you’re reading about finance elsewhere, assume all rates are annual.

Assigning Value with TVM

We’ll start with arbitrary round numbers for our variables in this section. In later sections we’ll explore how to determine things like the discount rate but for now take the rate as given.

Let’s say we have $100 today, and our discount rate is 5%. What’s the value of our money next year?

Here is the formula to “discount” value year-over-year:

You are dividing your amount by 1 + the discount rate

In other words, given a 5% discount rate, $100 today will be worth the same as $95.24 in one year

Expanding Our Understanding of TVM

We can keep going with this concept and compare $100 today to two years from now, three years, and so on

If we do that through a multi-year exercise, the discounting will be compounded. Compounding is one of the most important concepts in all of finance. It is so important that Albert Einstein himself took notice of the power of the laws of compounding

In our last example, at the end of year one, $100 turned into $95.24 with a 5% discount rate. For year two, you will discount 5% off $95.24 (not $100!), giving you $90.70 at the end of year two. Notice that this is not the same as simply taking 10% off $100 for two years worth of calculating - don’t do that when dealing with TVM.

Compounding is probably more intuitive when thinking in terms of investment returns. Let’s say we take that same $100 but invest it somewhere that gives us 5% return annually. 5% of $100 is $5, but due to the impact of compounding, you will earn far more than $5 per year over time, since each year you are compounding the returns off a higher and higher base.

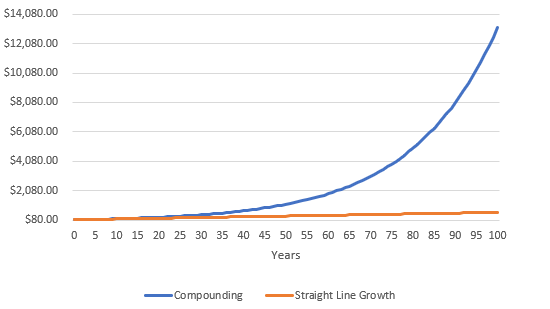
Take a look at the impact of compounding below, showing the growth of $100 at 5% annually vs. the growth of $100 at $5 annually. Importantly, compounding is exponential, meaning that its impact grows in magnitude as you move farther out in time. After two years, the difference in the two comparisons is $0.25, but after ten years, the divergence increases to $12.89

And to demonstrate what Einstein was talking about in terms of how truly powerful compounding can be, let’s extend that exact same graph out 100 years as a demonstration. Here is what it would look like.

$13,000 vs. $600; now you are truly seeing how powerful compounding can be!